최단 강하선(Brachistochrone) 문제와 사이클로이드(cycloid)

(질문답변 게시판에 최단강하선 관련 질문이 올라왔는데, 마침 예전에 써둔 글이 있어 공유해봅니다.)

1. 역사적 단상

• 갈릴레오는 (중심각이 $90^\circ$인) 원호 모양의 철사에 구슬을 꿰었을 때, 마찰없이 구슬이 미끄러지는데 걸리는 시간을 생각하였다. 미적분의 이론을 통해 구슬의 강하시간을 계산하면 \[ \sqrt{\frac{L}{g}}\int_0^{\pi/2}\frac{1}{\sqrt{1-\sin^2\left(\frac{1}{2}\alpha\right)\sin^2\beta}}\ \mathrm{d}\beta \] 이고, 이는 약 $1.8541\sqrt{L/g}$이다.
• 갈릴레오는 원호를 다각선으로 근사시켰을 때의 구슬의 낙하시간은 항상 [원호를 따라 낙하하는 구슬]의 낙하시간보다 크다고 추론하였다. (자세한 내용이 참고도서 [2]의 6.1절에 소개되어있다.) 어떤 사람들은 갈릴레오가 최단강하선이 원호임을 주장했다고 하는데, 이는 역사학자들 사이에 여러 이견이 있는 듯 하다.
• 요한 베르누이는 1696년 학술지 『Acta Eruditorum』에서 ‘세계에서 가장 뛰어난 수학자들(the most brilliant mathematicians in the world)’을 향해 다음과 같은 문제를 제시하였다. (이 학술지는 1682년에 처음으로 출판된 독일 최초의 학술지이다.)

  어떤 물체가 점 $\mathrm{A}$에서 출발하여 점 $\mathrm{B}$까지 중력에 의해서만 이동할 때, 소요시간을 최소화하려면 이 물체는 어떤 경로를 따라 이동해야 하는가?

  이 문제에 대해, 야곱 베르누이, 라이프니츠, 로피탈 등 여러 수학자가 옳은 답을 제시하였다. 그리고 익명으로 투고된 답안도 있었다. 요한은 이 답안을 보고 “발톱 자국으로부터 그것이 사자의 것임을 알 수 있다.”라고 말했다고 한다.^[5]
• 베르누이의 도전은 결코 호의적이지 않았다. 그리고 베르누이는 갈릴레오의 업적은 전혀 언급하지 않았으며, 오히려 최단강하에 관해 갈릴레오의 업적은 전혀 알지 못했었다고 주장했다. 또한 베르누이는 뉴턴과 사이가 좋지 못했는데, 이 최단강하선의 풀이에 대한 찬사가, 뉴턴을 향한 거의 유일한 좋은 평가라고 한다.^[2] 사실 요한 베르누이는 미적분학의 창시자가 누구인가에 대한 싸움에서 라이프니츠의 편에서서 전투적인 모습을 보였었다고 한다.^[4]

2. 준비학습: 에너지 보존법칙

• 질량이 $m$인 물체가 $v=y'(t)$의 속도로 자유낙하하고 있을 때, 이 물체의 운동에너지는 \[\frac{1}{2}mv^2=\frac{1}{2}m(y'(t))^2\]으로 정의되며, 이 물체의 위치에너지는 $mgy(t)$로 정의된다. 그리고 운동에너지와 위치에너지의 합을 역학적 에너지라고 한다.
• 중력에 의해서 자유낙하하는 물체의 가속도는 $y''(t)=-g$이다. 역학적 에너지를 시간 $t$에 대하여 미분해보면 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m(y'(t))^2+mgy(t)\right) &= my'(t)y''(t)+mgy'(t) \\ &= -mgy'(t)+mgy'(t)=0 \end{align*} 임을 알 수 있다. 따라서 역학적 에너지의 총량은 시간에 따라 변하지 않음을 알 수 있다.
• 중력장 안에서 $3$차원 운동을 하고 있는 질량 $m$인 물체의 시각 \(t\)에서의 위치를 \[\mathbf{X}(t)=(x(t), y(t), z(t))\]라 하면, 이 물체의 운동에너지는 \[ \frac{1}{2}m\Vert \mathbf{X}'(t)\Vert^2 \] 위치에너지는 \[ mgz(t) \] 이다. 중력에 의해서만 운동하는 이 물체의 역학적 에너지를 시간에 대해 미분해보면 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m\Vert \mathbf{X}'(t)\Vert^2+mgz(t)\right) & = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m(\mathbf{X}'(t)\cdot \mathbf{X}'(t))+mgz(t)\right) \\[4pt] & = m (\mathbf{X}'(t)\cdot \mathbf{X}''(t))+mgz'(t) \\[8pt] & = m\left( (x'(t), y'(t), z'(t))\cdot (0, 0, -g)\right)+mgz'(t) \\[8pt] &= -mgz'(t)+mgz'(t)=0 \end{align*} 으로 역시 역학적 에너지는 시간에 따라 변하지 않음을 알 수 있다.
• 물체의 운동을 살펴볼 때, 물체가 가진 속도, 에너지 등 물리적인 정보를 해석하기 위해서는 그 물체에 작용하는 모든 힘을 고려해야한다. 지금 살펴보고 있는 운동에서는
  1. 마찰력이나 공기의 저항은 무시하고 있다.
  2. 중력의 영향을 고려하고 있다.
  3. 철사 혹은 미끄럼틀 같은 경로를 정해주어 물체의 이동에 영향을 주고 있다.
  정도를 생각해볼 수 있다. 그런데, 물체가 가진 에너지에 대해서는 (c)의 영향을 고려하지 않아도 된다. 왜냐하면, 소위 ‘구속된 운동’에서의 구속력은 늘 물체의 이동방향에 수직으로 작용하므로 그 구속력이 하는 일은 늘 $0$이기 때문이다.

3. 베르누이의 풀이

스넬의 법칙을 상기해보자.

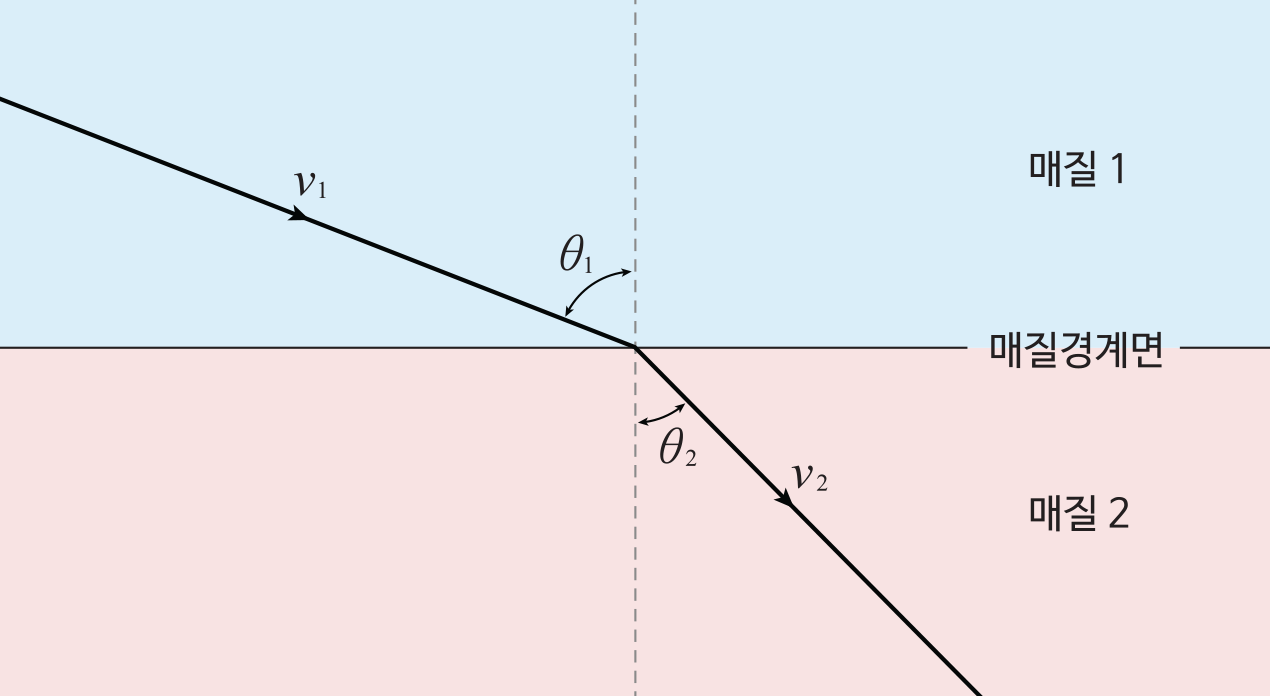
그림과 같이 서로 다른 매질1, 매질2가 있고 각각을 통과할 때의 속력이 $v_1, v_2$라고 할 때, B에서 A로 가는 빛의 경로는 \[ \frac{\sin\theta_1}{v_1}=\frac{\sin\theta_2}{v_2} \] 를 만족시킨다. 최단 강하선 문제에 대한 요한 베르누이의 풀이는 에너지 보존 법칙과 스넬의 법칙을 이용한 풀이이다.

이제 베르누이의 풀이를 살펴보자. 먼저 최단 강하선 $y=f(x)$가 있을 때, 이 곡선이 만족시켜야 하는 조건이 무엇인지 살펴보자. 편의상 $y$축의 방향을 아래쪽으로 향하게 하고(즉 $y$축의 방향을 속력이 증가하는 방향으로 두고) 점 $\mathrm{A}$를 원점에 위치시키자.

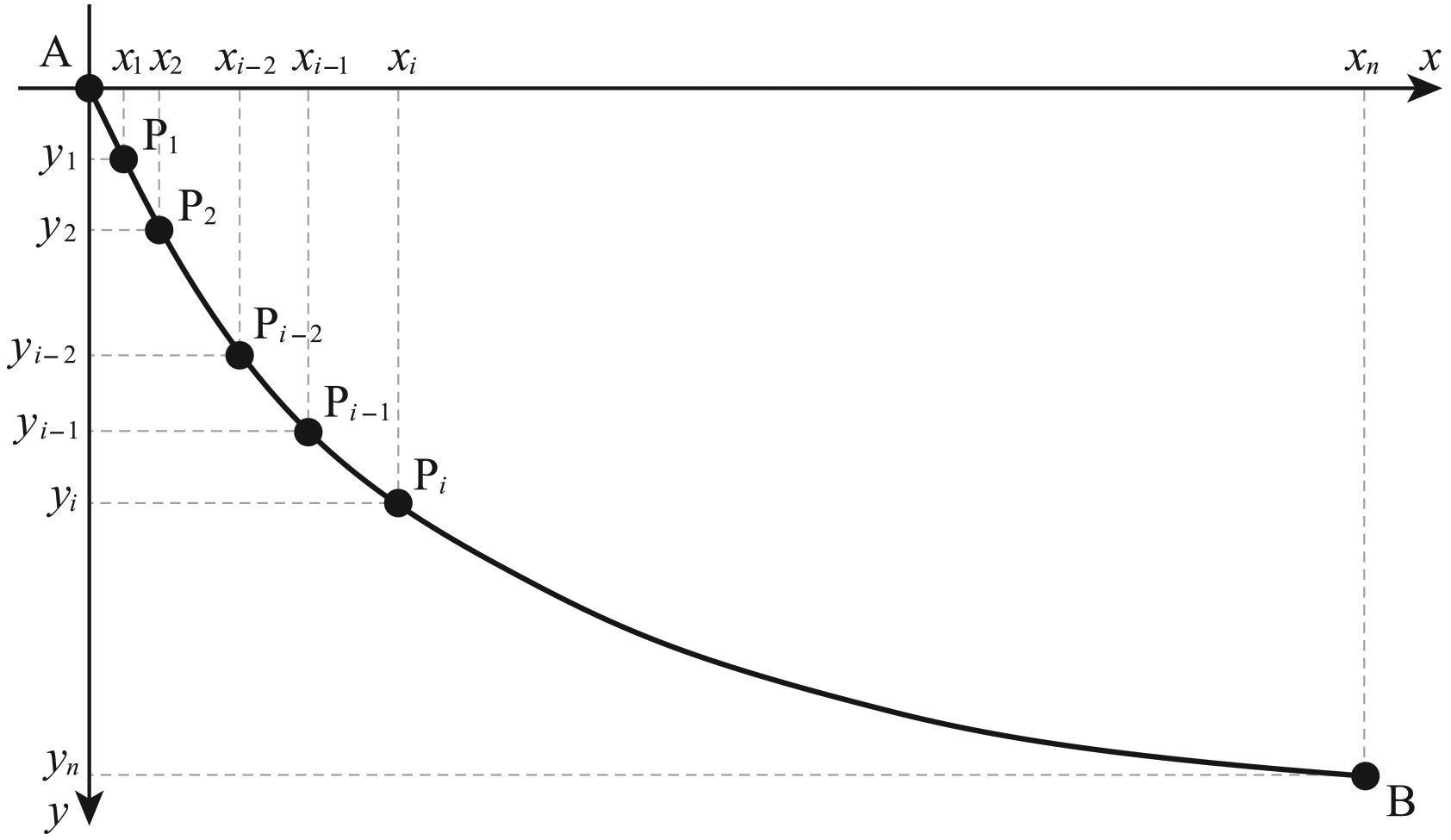
그리고 점 $\mathrm{B}$의 좌표는 $(b_1, b_2)$로 쓰자. 그림과 같이 $y$축을 $n$등분하는 가로선들을 그어, 이 가로선이 최단강하선과 만나는 점들을 $\mathrm{P}_i(x_i, y_i)$로 쓰자(단, $i=1,\,\ldots,\,n$). 물론 $\mathrm{A}=\mathrm{P}_0$, $\mathrm{B}=\mathrm{P}_n$이다.

베르누이는 그림에서 가로선들을 서로 다른 매질들의 경계면으로 생각하였다. 즉 최단강하선의 문제를 아래로 갈수록 덜 조밀한(즉 아래로 갈 수록 빛이 더 빠르게 이동할 수 있는) 여러 개의 층이 있을 때, 빛이 어떻게 이동하는가에 대한 문제를 통해 살펴본 것이다.

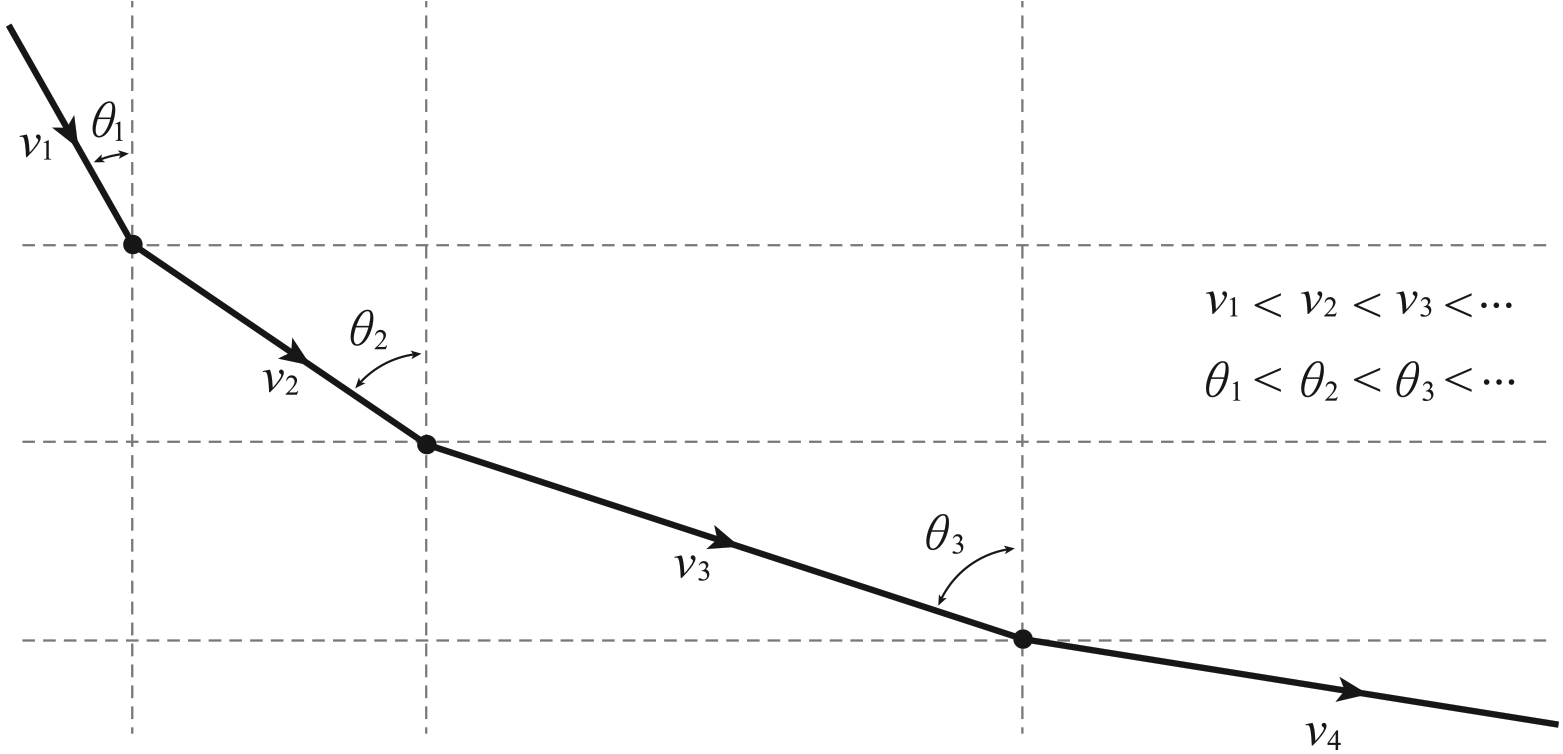
그림의 경로가 빛의 경로, 즉 소요시간을 최소화하는 경로라면, 역시 스넬의 법칙에 따라 모든 $i$에 대하여 \[ \frac{\sin\theta_{i-1}}{v_{i-1}}=\frac{\sin\theta_i}{v_i} \] 가 성립한다. 따라서 \[ \frac{\sin\theta_i}{v_i}=\mbox{(상수)} \] 로 둘 수 있다. 이제 층의 개수를 무한히 증가시키면 빛의 경로는 부드러운 곡선을 따르게 되는데, 그림과 같이 각 점에서의 속력 $v$에 대하여 등식 \begin{equation} \frac{\sin\theta}{v}=\mbox{(상수)}\tag{1} \end{equation} 가 성립한다.

이때 점 $\mathrm{P}(x, y)$에서의 속력 $v$는 에너지 보존 법칙을 이용해 구할 수 있다. 에너지 보존 법칙에 따르면, 물체가 낙하하면서 줄어든 위치 에너지만큼 그 물체가 가진 운동에너지가 증가한다. 그런데 점 $\mathrm{P}(x, y)$에서 처음에 비해 줄어든 위치에너지는 $mgy$이고 $\mathrm{P}_0$에서 이 물체가 가진 운동에너지가 $0$이었으므로 늘어난 운동 에너지는 $\frac{1}{2}mv^2$이고 이는 $mgy$와 같다. 따라서 \begin{equation} v=\sqrt{2gy}\tag{2} \end{equation} 가 성립한다. 위의 그림에서와 같이 접선이 가로선과 이루는 각을 $\alpha$라 하면, $\theta+\alpha=\pi/2$이고 따라서 \begin{align*} \sin\theta&=\cos\alpha=\frac{1}{\sec\alpha}=\frac{1}{\sqrt{1+\tan^2\alpha}} \\ & = \frac{1}{\sqrt{1+(\mathrm{d}y/\mathrm{d}x)^2})}=\frac{1}{\sqrt{1+(y')^2}} \end{align*} 이 성립한다. 이 결과와 식 (1), (2)를 이용하여 \[ (\mbox{상수})=\frac{\sin\theta}{v}=\frac{\frac{1}{\sqrt{1+(y')^2}}}{\sqrt{2gy}}=\frac{1}{\sqrt{2gy}\sqrt{1+(y')^2}} \] 을 얻는다. 이로부터 최단 강하선이 만족시키는 미분방정식 \[ y(1+(y')^2)=C\tag{3} \] 를 얻는다. (단, \(C\)는 상수.)

일반적으로 선형이 아닌 미분방정식은 해를 구하는 것이 쉽지는 않지만, 식 (3)은 변수분리형 미분방정식으로 해를 구할 수 있다. 실제로 식 (3)을 \[ \mathrm{d}x=\mathrm{d}y\sqrt{\frac{y}{C-y}} \] 로 변형하고, $\tan\varphi=\sqrt{\frac{y}{C-y}}$로 두면 \begin{align*} &\frac{y}{C-y}=\tan^2\varphi=\frac{\sin^2\varphi}{\cos^2\varphi}\\[5pt] \Rightarrow\quad & y\cos^2\varphi =C\sin^2\varphi -y\sin^2\varphi \\[8pt] \Rightarrow\quad & y=C\sin^2\varphi \end{align*} 를 얻는다. 이제 $x$를 매개변수 $\varphi$로 나타낼 수 있으면, 곡선 $y=f(x)$의 매개변수 표현을 얻는 것이 된다. 위의 마지막 식을 미분하여 $\mathrm{d}y=2C\sin\varphi\cos\varphi\ \mathrm{d}\varphi$를 얻고 이를 이용해 \begin{align*} \mathrm{d}x&=\mathrm{d}y\sqrt{\frac{y}{C-y}}=2C\sin\varphi\cos\varphi\tan\varphi\ \mathrm{d}\varphi \\[5pt] &= 2C\sin^2\varphi\ \mathrm{d}\varphi \\[8pt] &= C(1-\cos(2\varphi))\ \mathrm{d}\varphi \end{align*} 즉 $\mathrm{d}x=C(1-\cos(2\varphi))\ \mathrm{d}\varphi$를 얻고, 양변을 적분하여 \[x=\frac{1}{2} C(2\varphi-\sin(2\varphi))+C_0\] 를 얻는다. 여기서 적분상수 $C_0$는 초기조건을 통해 $0$임을 바로 알 수 있다. 이제 $2\varphi=\theta,$ $R=\frac{1}{2}C$로 두면 곡선 $y=f(x)$의 매개변수 표현 \[ x=R(\theta-\sin\theta),\quad y=%C\sin^2\varphi=\frac{1}{2}C(1-\cos(2\varphi))= R(1-\cos\theta) \] 를 얻는다. 이는 그 유명한 사이클로이드 곡선의 매개변수 표현이다.

• 상수 $R$을 적절히 조절하면, 임의의 점 $(x, y)$ (단, $x>0, y>0$)를 지나는 사이클로이드를 정할 수 있다.
• 베르누이의 풀이를 다시 살펴보면, 다음의 두 가지 가정이 중요한 역할을 하고 있음을 알 수 있다. 그리고 이 가정들은 타당하다고 생각된다.
  • 곡선 $ y=f(x)$를 각 $\mathrm{P}_i$를 잇는 선분 경로들의 모임으로 근사시켜서 생각한다. ($n$이 충분히 클 때, 이는 실제 물체의 운동에 대한 좋은 근사가 된다.)
  • 물체가 $\mathrm{P}_{i-1}$에서 $\mathrm{P}_i$까지 직선경로를 따르며 이동하는 속력이 $v_i$로 일정하다고 가정한다.

4. 오일러-라그랑지 방정식과 변분법

점 $\mathrm{P}_{i-1}$에서 $\mathrm{P}_i$까지 ($v_i$의 속력으로) 이동하며 걸리는 시간을 $T_{i-1}^i$라 하면, 최단강하선 문제는 \[ \lim_{n\to\infty}\sum_{i=1}^{n}T_{i-1}^i \] 를 최소화 하는 것이다. 특히 $T_{i-1}^i=\frac{\overline{\mathrm{P}_{i-1}\mathrm{P}_i}}{v_i}$이므로 위 식을 다시 쓰면 \begin{align*} \lim_{n\to\infty}\sum_{i=1}^{n}T_{i-1}^i&=\lim_{n\to\infty}\sum_{k=1}^n \frac{\sqrt{\Delta x_i^2+\Delta y_i^2}}{v_i} \\ & = \lim_{n\to\infty}\sum_{i=1}^n \frac{\sqrt{1+(\Delta y_i/\Delta x_i)^2}}{\sqrt{2gy_i}}\cdot \Delta x_i \end{align*} 이다. 즉 최단강하선 문제는 \[ \int_0^{b_1}\frac{\sqrt{1+(y')^2}}{\sqrt{2gy}} \mathrm{d}x \] 를 최소화하는 문제이다. 다시 말해,

주어진 경로에 따르는 소요시간을 재는 함수 $T$를 생각할 때, $T$가 최소가 되는 $y=f(x)$가 무엇인가?

가 궁금한 것이다. 여기서 $T$는 곡선(함수)을 실수로 대응시키는 범함수이다. 이처럼 범함수의 극대, 극소(혹은 최대, 최소)를 찾는 기법을 변분법이라고 부른다.

미분가능한 함수 $f:[0, b_1]\to\mathbb{R}$와 이변수 함수 \[\mathscr{L}(u, v):=\frac{\sqrt{1+v^2}}{\sqrt{2gu}}\]를 생각할 때, 이를 이용하여 얻은 범함수 \[ T(f)=\int_0^{b_1}\mathscr{L}(f(x), f'(x)) \mathrm{d}x% =\int_0^{b_1}\frac{\sqrt{1+(f'(x))^2}}{\sqrt{2gf(x)}} \mathrm{d}x \] 의 최솟값을 생각하는 것이 바로 최단강하선 문제이다.

$T$는 함수들의 집합 $\mathscr{F}=\{ f\in C^\infty[0, b_1]\mid f(0)=0, f(b_1)=b_2\} $에서 정의된 범함수이다. 만일 $f$가 $T$를 최소가 되게 하는 함수라면, 임계점 정리에 의해, 임의의 함수 \[ h:[0, b_1]\to \mathbb{R},\quad h(0)=0, h(b_1)=0 \] 에 대하여, \[ g(t):=\int_0^{b_1}\mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \] 는 $t=0$에서 최솟값을 갖는다. 따라서 \begin{align*} 0=g'(0)&= \frac{\mathrm{d}}{\mathrm{d}t}\Big\vert_{t=0} \int_0^{b_1}\mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \\ &= \int_0^{b_1} \frac{\mathrm{d}}{\mathrm{d}t}\Big\vert_{t=0} \mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \\ &= \int_0^{b_1} \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x) )\cdot h(x)+\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\cdot h'(x)\ \mathrm{d}x \\ &= \int_0^{b_1}\left( \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))-\frac{\mathrm{d}}{\mathrm{d} x}\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\right)h(x)\ \mathrm{d}x \end{align*} 가 성립한다. 여기서 가장 마지막 줄의 등호는 부분적분 및 $h(b_1)=h(0)=0$을 이용하여 얻은 등식 \begin{align*} \int_a^{b_1}\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h'(x)\mathrm{d}x &= \left.\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\right\vert_0^{b_1}\\ &\qquad\qquad - \int_a^{b_1} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\mathrm{d}x \\ &= - \int_a^{b_1} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\mathrm{d}x \end{align*} 를 사용하였다. 이때 $h$는 임의의 함수이므로 방정식 \begin{equation} \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))=\frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\tag{4} \end{equation} 를 얻는다. $T$의 극값이 되는 함수 $y=f(x)$는 방정식 (4)를 만족시켜야 한다. 방정식 (4)를 오일러-라그랑지 방정식이라 부른다.

오일러-라그랑지 방정식의 양변에 $f'(x)$를 곱하면 \[ f'(x) \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))=f'(x) \frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x)) \] 이고, 이 식에 다시 $f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x))$를 더하여 \begin{align*} f'(x) \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x)) +& f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x)) \\ &=f'(x) \frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))+f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x)) \end{align*} 를 얻는데, 이를 다시 쓰면 \[ \frac{\mathrm{d}}{\mathrm{d}x}\mathscr{L}(f(x), f'(x))=\frac{\mathrm{d}}{\mathrm{d}x}\left( f'(x) \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\right) \] 이다. 따라서 \begin{equation} \mathscr{L}(f(x), f'(x))=f'(x)\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))+C\tag{5} \end{equation} 를 얻는다. 특히 $\mathscr{L}(u, v)=\frac{\sqrt{1+v^2}}{\sqrt{2gu}}$이므로 $\frac{\partial}{\partial v}\mathscr{L}(u, v)=\frac{v}{\sqrt{2gu}\sqrt{1+v^2}}$이고 이를 식 (5)에 대입하여 \[ \frac{\sqrt{1+(f'(x))^2}}{\sqrt{2gf(x)}}=f'(x)\cdot \frac{f'(x)}{\sqrt{2gf(x)}\sqrt{1+(f'(x))^2}}+C \] 를 얻는다. 이 식을 정리하면 베르누이의 풀이에서 얻은 것과 동일한 미분방정식인 \[ y(1+(y')^2)=\text{Const.} \] 를 얻는다.

참고한 글

1. 윤종국, 현대기하학 강의록(최소 하강선과 변분법)
2. Paul J. Nahin, When Least is Best, Princeton University Press, (2004) / 번역서: 최상의최소(경문사/권오남 외)
3. 김홍종, 미적분학2+, 서울대학교 출판부, (2017)
4. William Dunham, The Calculus Gallery, Princeton University Press, (2005) / 번역서: 미적분학 갤러리(청문각/권혜승)
5. Wikipedia, https://en.wikipedia.org/wiki/Brachistochrone_curve